|
您当前的位置: 气体分离设备商务网 → 行业书库 → 在线书籍 → 《气体爆炸手册(GAS EXPLOSION HANDBOOK )》
Response of StructuresTo predict explosion pressure is one step in a consequence analysis. The next step is to estimate the response of the structures subjected to the load from the gas explosion. Knowledge about structural response is therefore also important in accident investigations. (See Chapter 14). Structural response is not a research activity which CMR has been heavily involved in. However, the area of loads acting on structures is under investigation. In our opinion there is little information available on loads and structural response from gas explosions. Today, the main source of information in this field is in blast effects from military weapon tests. These data are not always directly applicable for accidental gas explosions. The objectives of this chapter are to: i) Describe the difference between a static load and a dynamic load acting on a structure. ii) Explain how the load from a gas explosion acts upon a structure. iii) Describe the typical damage and response of equipment and buildings when subjected to explosion pressure loads.
8.1 Dynamic Response A gas explosion is a very rapid event. In a large gas explosion, the overpressure duration will typically be 100200 msec. The load from a gas explosion is therefore a dynamic load. To illustrate the difference between a static load and a dynamic load we will use a single-degree-of-freedom system as an example. A house subjected to a blast wave can be reduced to a single-degree-of-freedom system. This is shown in Figure 8.1.
The pitched roof is reduced to a rigid beam and the walls are treated as vertical cantilevers. This can further be reduced to a simple mass spring system. The load, i.e. pressure-time area, is simplified to a triangular pulse. The response x, i.e. the displacement of mass m, will depend on the maximum force, the natural frequency of the system, T = 2p(m/k)1/2, and the mass m. The displacement can be predicted by Newton's second law: mass * acceleration = force. The result of such a calculation is shown in Figure 8.2.
In this system there is no damping. The mass therefore continues to oscillate. In real situations there will always be some damping and the mass will come to a rest after a while. However, it is important to recognise that the maximum displacement of the mass, Xmax dynamic , will depend on the ratio of the duration of load, tL, and the natural frequency of the system, T. For low tL /T ratio, the Xmax dynamic is smaller than the displacement for the static load (Xstatic = F/K). For larger tL/T-ratios, Xmax dynamic can be larger than the displacement for static loads. Figure 8.3 shows the ratio of Xmax dynamic/ Xstatic [also called the dynamic load factor (DLF)] versus tL/T for two different types of triangular loads.
Actual structures may have many degrees of freedom and prediction of their behaviour needs detailed analysis. A single-degree-of-freedom system is very simplified, but it illustrates the basic behaviour of structures subjected to a dynamic load. The structural response and damage level will depend on the load (i.e. pressure and/or drag) as a function of time and the structure's own characteristics.
8.2 Loads from Gas Explosions A gas explosion will generate high pressures and often also high flow velocities. It is the pressure and flow that cause the dynamic load on structures and consequently cause the damage. Inside an exploding gas cloud the type of load as generated by a gas explosion simulation will depend on the size of the structure. A wall can be spatially resolved by the simulation code. The main load from the explosion, the pressure, will therefore be calculated directly by the code. A small pipe standing in the explosion, however, will not be resolved by the code and the pressure differential can not be directly calculated. The load will have to be calculated by reference to the flow conditions (velocity and density) using a drag formula. A pressure-time curve for a gas explosion in a compartment is shown in Figure 8.4.
The pressure will be close to zero in the initial phase of the explosion when the burning rate is low. When the flame starts to accelerate the pressure rises rapidly and the maximum pressure will be reached. The pressure will then drop as the burning rate decreases and the gas is relieved through the vent openings. Due to the inertia of the flow the pressure of the burnt gas will drop below the ambient pressure. The main parameters that will influence structural response are: maximum pressure, the pressure rise time (dp/dt), the positive impulse and the negative impulse. The impulse is the time integral of pressure which takes both the pressure and the duration of the pulse into account. The importance of the negative impulse will depend very much on the natural frequency of the structure. If the negative pressure is in the phase with vibration of the structure, the negative phase can have a significant contribution. The negative impulse can be about 1/3 of the positive impulse phase, but this ratio depends on the layout of the geometry where the explosion occurs. The results from gas explosion analyses or experimental results are often reported as maximum pressure. The maximum pressure is a very important parameter, but rise time, impulse and duration can also be important. It should also be noted that accurate values for maximum pressure are not always easy to read from a record due to the often spiky nature of the pressure signal. The high spikes that are observed both in experiments and FLACS-simulations may be of importance in estimating structural response. The topology of the pressure load (the distribution in time and space) may also be important. These areas are still under investigation. It is presently not clear what level of information is required to perform detailed analyses. As explained above, smaller objects like piping which are inside an exploding gas cloud, will be subjected to drag force. In fluid dynamics drag force is often estimated from the formula: FDrag = CDA * 0.5ru2 CD is the drag coefficient, A [m2] is the projected area of the object normal to the flow direction and 0.5ru2 is the dynamic pressure. For objects large enough to be resolved by the simulation code used to predict the gas explosion, the pressure differential is calculated directly. For non-stationary loads from gas explosions there are still uncertainties with regard to estimating drag load. The drag coefficient will probably be dependent on several factors such as turbulence level, time, pressure rise time etc. CMR has lately performed some pilot tests with a 0.168 m diameter pipe in the exit of a wedge shaped vessel. (Sand et al., 1992). The explosion pressure and load are shown in Figure 8.5.
As discussed in Chapter 7, an explosion will cause the blast wave to propagate away from the explosion area. We call this blast wave, which is outside the explosion area, the free field blast (see Figure 7.1). When the wave hits a building or another object, the wave and the object will interact. One effect of this is that the shock wave (i.e. front of a strong blast wave) will be reflected, as shown in Figure 8.6.
When the shock wave hits the wall, the gas behind the shock wave has to come to a rest (i.e. u = 0 m/s) to satisfy the boundary conditions. The actual (reflected) pressure will then consist of the sum of the incident blast pressure and the dynamic pressure (i.e. 0.5ru2). For a shock wave with incident pressure of 1 barg, the reflected pressure will be approximately 2.7 barg. For incident pressure of a few hundred millibars, the reflected pressure is approximately twice the incident pressure (in this paragraph pressure means overpressure). If a small object is subjected to a free field blast with a shock front, the first phase of the loading will be due to the reflected pressure. The duration of this phase is the time the shock wave takes to pass the object (i.e. object dimension / shock velocity). When the shock wave has passed the object, the object will feel the wind load (i.e. drag) from the blast wave (see Figure 8.7).
Further details about shock reflection and drag from blast waves can be found in Baker et al. (1983). 8.3 Damage Level The objective of this section is to list some available data on damage levels for typical process equipment. The data included here are general and should not be used as exact values, but as indications of damage level. A lot of the available data comes from military sources and are based on experience from blast waves for high explosives and nuclear explosions. To our knowledge there are limited data available on structure response to actual gas explosions. However, we expect that the future will bring more exact data. Data including both impulse and pressure are needed. Stephens (1970) has presented damage level to vulnerable refinery parts. These data are given in Table 8.1. From this figure we see that the damage starts around 100 mbarg and the damage becomes very serious from 0.5 - 1.0 barg.
Code:
8.4 Damage to Buildings Figure 8.8 shows damage levels to brick buildings versus peak pressure and impulse of the blast wave from high explosives. These data were obtained from the London area at the end of World War II. Baker et al. (1983) claim that this diagram also can be used for other homes, small office buildings and light frame industrial buildings.
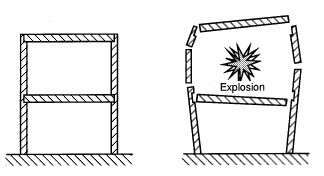
An important aspect of damage to buildings is whether the integrity of buildings survives. Damage to a building in case of an accidental gas explosion is not a serious problem as long as the building is not collapsing or dangerous fragments are generated within or from the building. This is equally important for buildings subjected to blast loads from the outside as well as buildings with possibilities of internal explosions. Figure 8.9 shows design of a building where an internal explosion will cause the building to collapse. Buildings made of pre-fabricated walls and roof will often collapse when subjected to explosion loads. As shown in Table 8.2 ordinary brick walls are also weak. In case of an internal explosion the brick wall will disintegrate and cause dangerous fragments.
Ordinary window glass will typically fail at 20 to 70 mbarg and cause dangerous flying fragments. As shown by Harris (1983), glass fragments can fly more than 20 m when the breaking pressure is about 0.25 barg. The velocity of these fragments will be up to 30 to 40 m/s. (~ 100 km/h). To use ordinary window glass in areas where there is an explosion hazard is not recommended. Use blast resistant glass and make the windows as small as possible. The window frames must be as strong as the window itself. If ordinary windows are replaced by blast resistant windows, the frame also has to be changed. If the frame is weaker than the window, the window will fly out as one piece. Some design criteria for buildings can be found in Figure 8.8. Guidelines for building design:
8.5 Domino Effects As a result of a violent gas explosion walls or decks may start to move or even break down and fragment. Pipes that are suspended on a moving wall may be sheared off (i.e. guillotine break) as a result of the relative movement of the points of suspension. Piping from one module to another module may have to respond to relative movements of the structure. Cables and control lines may also be damaged due to this type of relative movement. Figure 8.10 illustrates how deflection and movement due to explosions may cause damage to piping.
8.6 Effect on People People can survive fairly strong blast waves. Lung damage data (Baker et al., 1983), show 1% survival for shock pressures of approximately 3.5 barg and 99% survival for shock pressures of about 2 barg for long duration blast. The threshold limit is about 0.7 barg. Eardrum rupture data show 10% rupture for peak pressures of about 0.25 barg. In accidental gas explosions there are very few cases where the blast has killed people directly. The Sarnia incident (London Free Press, 1984), where two persons were killed because of a detonating hydrogen-air cloud is one of these cases. When people are killed or injured in gas explosions the injuries are typically caused by:
Protecting people from injuries is therefore linked to designing structures. Structures should be designed to withstand loads without creating dangerous fragments or falling down. 注意:本栏目所有书籍均来至于网络,如果其中涉及了您的版权,请及时联系我们,我们在核实后将在第一时间予以删除!
|